辐射测量的理论基础

黑体辐射

物体的辐射本领是相对于同温度下的理想辐射源（通常称作绝对黑体）而言的。绝对黑体吸收其接受的全部能量并且在同样的温度下，其总辐射通量或任意光谱区间的波段辐射通量都比其他辐射体大。

虽然绝对黑体是一个理想化的模型，严格意义上说不存在这样完美的辐射源。但实验室设计特殊构造的光源辐射效率通常会远高于98%甚至达到99.98%。最常用的方法是采用用表面开有小孔的球型空腔或者用长径比大的密封柱形腔体设计并且使不透明的腔体处于均匀恒定的温度。

如图1所示的结构保证了入射到小孔的的辐射能够多次反射。尽管球体或管壁有轻微反射，但是在多次反射之后，几乎所有能量都被吸收了，例如把内表面涂黑，假设表面吸收率为0.9，反射率为0.1，经三次反射后它就吸收了入射光的0.999，已经非常接近黑体了。因此，只要满足腔壁近似等温，开孔比腔体小得多，就有可能制作一个黑体源。

另外一种黑体结构是用于面源设计的深楔形结构，锥角的角度非常小，楔形侧面多次反射使其表面看起来很黑。可以将物体的表面粗糙度看作机械加工表面或铸件中的许多小楔块。如果表面非常粗糙，则楔形很深，与光滑表面相比，辐射特性更接近黑体。

斯蒂芬-波耳兹曼定律

黑体的辐射通量密度由斯蒂芬-波耳兹曼定律给定:

该等式假设接收辐射的物体绝对为零。实际情况下，接收辐射的物体处于温度T R，辐射到黑体的辐射通量密度为：

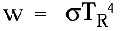
这样的话，接受辐射的物体单位面积上实际感应的辐射通量为:

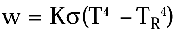
其中 K 是一个常数，具体取值要考虑黑体和接收辐射的物体的面积以及它们之间的距离。
上述等式给出的是在整个波长范围内的全部辐射通量密度。多数情况下接受辐射的物体（例如高温计中的探测器）仅对辐射波段中的短波有明显响应，维恩-普朗克定律则更为有用。

维恩-普朗克定律

维恩-普朗克定律表述的是黑体单位面积发出的辐射与波长, λ, 和绝对温度, T.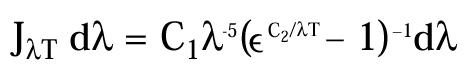

图四给出了几个温度下波长与温度的关系图。

C1, 第一辐射常数 = 3.7418 x 10-16 watts/m2

C2 第二辐射常数 = 1.43879 x 102 m · K 

维恩定律

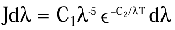
如果C2/ λ T 远大于1, 维恩-普朗克定律近似于维恩定律.

如果 λT小于 0.003 m · K (3000m m.K)，则该表达式与维恩定律仅有1%偏差.

在0.65 μm 波段, 温度低于 4600K的条件下能很好地满足上述条件. 因此，在光学高温测量领域中，维恩定律已被广泛使用。.
 

维恩位移定律

在图4中可以看出，随着温度的升高，不仅单位面积的辐射量增加，而且辐射最大值所在波长也向短波方向偏移。

每单位面积最大辐射对应的波长值由维恩位移法给出：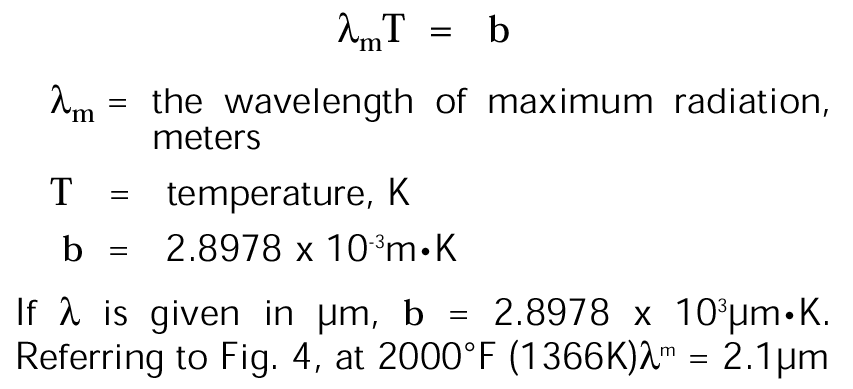

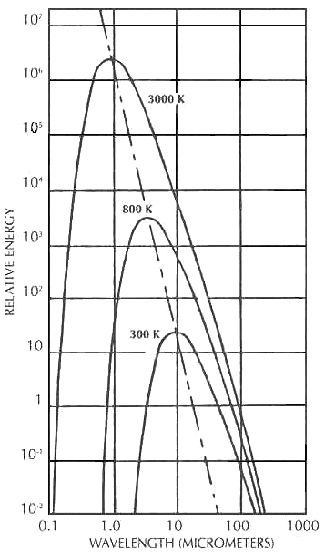
Fig. 4 辐射强度与波长和温度的关系 (Planck’s Law)

校准几何公式

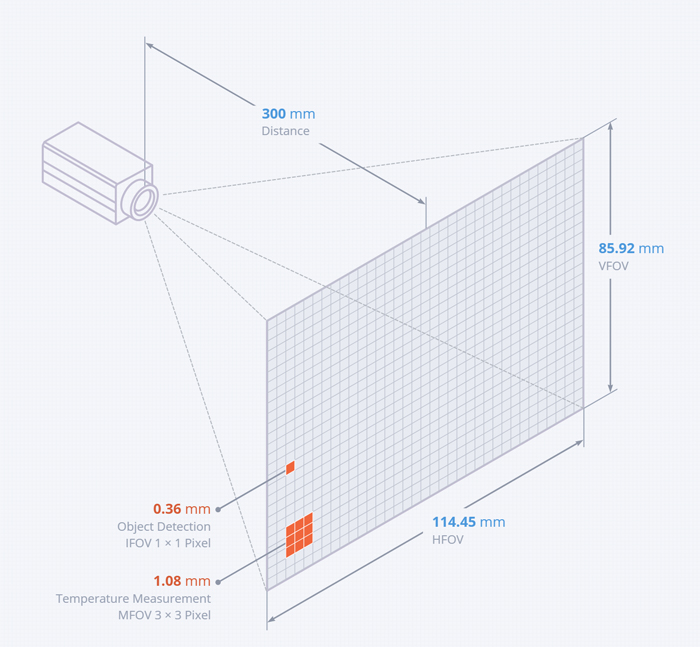
所有的高温计，特别是哪些长波高温计，都有“尺寸效应（SSE）“，即测量距离一定时，高温计的输出依赖于被测物大小的效应。这意味着高温计的输出特性与视场外的背景辐射有关。这是由辐射温度计光学系统中灰尘等引起的散射、透镜表面间的反射、光学系统的像差及衍射等效应的综合结果。

如果用刚好等于高温计的光斑大小辐射源作为参考，对于那些使用大尺寸辐射源的人会获取非常高的读数。另方面如果以大尺寸的辐射源作为参考，使用小尺寸辐射源的人会得到一个相对低的读数。

VDI/VDE 3511 第 4.4 部分的官方校准规范将“校准直径”定义为这两个极端位置之间的实际折衷。我们提供的产品也参照此方案校准。